Dit verslag behelst het onderzoek naar Value-at-Risk en parameteronzekerheid. Value-at-Risk is een veel gebruikte maatstaf om risico's weer te geven. Met behulp van schattingen voor VaR kan een instelling inschatten wat het risico is dat zij loopt met een bepaalde handeling. Value-at-Risk komt oorspronkelijk uit de beleggingssfeer om het risico van een optieportefeuille te berekenen, maar wordt tegenwoordig op vele andere gebieden gebruikt. Dit verslag geeft een inleiding op het onderzoek dat plaatsvindt naar het negeren van parameteronzekerheid in Value-at-Risk aan de hand van de CBS-index en de Standard & Poor 500 index.

Voor een duidelijk beeld van het begrip Value-at-Risk beginnen wij dit verslag met enkele definities en een overzicht van de belangrijkste technieken. Vervolgens zal in hoofdstuk 2 aandacht worden besteed aan de gebruikte data. In hoofdstuk 3 worden deze data geanalyseerd om uiteindelijk in hoofdstuk 4 de Value-at-Risk te berekenen. Tenslotte zal in hoofdstuk 5 een korte inleiding worden gegeven in de theorie van de ARCH en GARCH-modellen, welke van belang zijn voor het uiteindelijke onderzoek.

Vanwege de beperkte uitgave mogelijkheden zijn de opgenomen tabellen en grafieken in dit rapport tot een minimum beperkt. Grafieken die niet opgenomen zijn kunnen bestudeerd worden op de volgende internet pagina: http://www.fortunecity.com/campus/law/672/ectrie4.html

In dit hoofdstuk zal het begrip Value-at-Risk nader worden verklaard door middel van enkele definities. Verder zullen enkele methoden en technieken ter sprake komen om de Value-at-Risk te berekenen. Tot slot zullen in de laatste paragraaf deze methoden worden vergeleken om te bepalen welke methode het best kan worden gebruikt bij verschillende criteria.

Ondernemingen en instellingen zijn geïnteresseerd in het financieel risico dat zij lopen gedurende een bepaalde periode. Dit is van belang om de continuïteit van de onderneming of instelling te kunnen waarborgen en inzicht te geven in de financiële situatie. Een veel gebruikte maatstaf om dit risico weer te geven is de Value-at-Risk (VaR).

Value-at-Risk is de waarde die gedurende een vooraf bepaalde tijdshorizon slechts met een kans van a % overschreden wordt.

Deze algemene definitie kan worden toegepast op verscheidene onderwerpen. Enkele voorbeelden zijn het berekenen van de waarde van een optie- of aandelenportefeuille, verwachte omzet of winst, balansposten.

Aan de hand van deze Value-at-Risk kan bekeken worden of er bepaalde maatregelen genomen moeten worden om het financiële risico van de onderneming of instelling te verminderen. Naast weergave van de financiële situatie kan Value-at-Risk gebruikt worden voor verschillende andere doeleinden, zoals modelevaluatie en het meten van opbrengsten op basis van aangepaste risico's.

Twee belangrijke keuzes bij de bepaling van de Value-at-Risk zijn de grootte van de overschrijdingskans(a ) en de lengte van de tijdshorizon(t). De overschrijdingskans is de kans dat de werkelijke waarde groter is dan de Value-at-Risk waarde. De overschrijdingskans is vrij te kiezen, maar veel gebruikte waarden zijn 1%, 2.5% en 5%. Deze keuze is afhankelijk van de risico-aversiteit van het desbetreffende bedrijf of instelling.

De keuze van de lengte van de tijdshorizon is afhankelijk van de tijd waarop men resultaat wil berekenen. Bovendien moet men rekening houden met de frequentie waarin veranderingen in de gegevens plaatsvinden.

In dit verslag zullen wij de Value-at-Risk bepalen voor twee verschillende beursindices. Bovenstaande definitie kan dan worden geschreven als definitie 2.

Value-at-Risk is het rendement van de index dat gedurende één dag slechts met een kans van a % overschreden wordt.

Er zijn een aantal verschillende manieren om de Value-at-Risk te berekenen. De drie varianten die wij zullen bespreken zijn de historische simulatie methode, de variantie covariantie methode en de Monte Carlo simulatie methode.

Historische simulatie is een gemakkelijke aanpak, waarvoor geen aannamen over de statistische verdeling van de onderliggende marktfactoren zijn vereist. Bij deze methode wordt gebruikt gemaakt van de historische veranderingen in marktfactoren om een verdeling van mogelijke toekomstige resultaten te construeren.

Historische simulatie kan aan de hand van het volgende stappenplan worden uitgevoerd:

1. Identificeer de marktfactoren die van belang zijn en bepaal een formule die de waarde van de portefeuille bepaalt.
2. Verzamel historische gegevens van de marktfactoren over de laatste N perioden.
3. Bereken voor iedere periode het resultaat van de portefeuille. Dus bereken de waarde van de portefeuille vandaag en bereken de waarde van de portefeuille gisteren. De waarde van vandaag minus de waarde van gisteren is dan het resultaat.
4. Orden de resultaten van klein naar groot.
5. Bepaal het resultaat dat in a % van de gevallen overschreden wordt. Dit is het resultaat behorende bij waarneming nummer a *(totaal aantal waarnemingen).

De variantie covariantie methode is gebaseerd op de aanname dat de onderliggende marktfactoren een multivariate normale verdeling hebben. Met behulp van deze aanname is het mogelijk een normale verdeling te bepalen van de resultaten. Aan de hand van de eigenschappen van de normale verdeling is het mogelijk om de Value-at-Risk te bepalen.

Deze methode bepaalt de waarde van de VaR aan de hand van het volgende stappenplan:

1. Bereken de huidige waarde van de portefeuille.
2. Bepaal de gevoeligheid van de portefeuille onderdelen voor de marktfactoren.
3. Schat de standaard deviaties en correlatiecoëfficiënten van de marktfactoren.
4. Bereken de standaard deviatie van de geschatte waarde van de portefeuille in de volgende periode.
5. VaR = N(a )*s .

Bij Monte Carlo simulatie worden geen historische gegevens gebruikt om de simulatie uit te voeren. Bij deze methode wordt een verdeling geformuleerd die de veranderingen in de marktfactoren beschrijft. Deze verdeling kan gekozen worden of aan de hand van de historische gegevens worden bepaald. Vervolgens wordt een groot aantal waarnemingen gesimuleerd door middel van trekkingen uit deze verdeling. Met behulp van deze simulaties is het mogelijk de VaR van de portefeuille te bepalen.

Bovenstaande berekening van de VaR kan worden samengevat in het volgende stappenplan:

1. Identificeer de marktfactoren die van belang zijn en bepaal een formule die de waarde van de portefeuille bepaalt.
2. Veronderstel een verdelingsfunctie (of bepaal deze aan de hand van de historische gegevens) voor de veranderingen in de marktfactoren. Schat vervolgens de parameters van deze verdeling
3. Genereer N trekkingen uit deze verdeling
4. Orden de resultaten van klein naar groot.
5. Bepaal het resultaat dat in a % van de gevallen overschreden wordt. Dit is het resultaat behorende bij waarneming nummer a *(totaal aantal waarnemingen).

De bovenstaande methoden en technieken hebben duidelijke verschillen in implementatiegemak, eenvoud van uitleg, de mogelijkheid tot het bevatten van de risico's van opties, flexibiliteit in analyseren van het effect van veranderingen in de aannamen en tot slot in de betrouwbaarheid van de resultaten.

De historische simulatie is de gemakkelijkste methode, omdat op basis van gesorteerde historische gegevens de VaR eenvoudig kan worden afgelezen. Bovendien is deze methode het best te gebruiken bij presentaties vanwege zijn simpliciteit. Nadeel van deze methode is dat als de dataset, waarop de VaR is gebaseerd, een aantal uitschieters bevat de kans bestaat dat de VaR-statistic één van die uitschieters kan bevatten. Dit resulteert in een waarde die niet representatief is voor de huidige marktomstandigheden. Een volgend nadeel is dat de historische simulatie erg afhankelijk is van de hoeveelheid waarnemingen. Bij een groter aantal waarnemingen wordt de invloed van uitschieters op de waarde van de VaR kleiner. Tot slot kan de periode waarop de waarde van de VaR is gebaseerd niet representatief zijn voor de komende periode.

Dit nadeel kan ook voor de variantie covariantie methode worden genoemd. De parameters van de normale verdeling worden namelijk geschat op basis van historische gegevens, welke niet representatief kunnen zijn voor de huidige marktomstandigheden. Een ander probleem is dat de risico's van opties niet adequaat kunnen worden samengevat voor VaR over een langere tijdshorizon dan één dag. Grote veranderingen in onderliggende waarden zorgen voor onbetrouwbare waarden van de VaR. De simulatiemethoden berekenen de waarde van de portefeuille iedere periode opnieuw, waardoor deze betere resultaten opleveren. Dit is de reden dat deze methoden worden geprefereerd boven de variantie covariantie methode indien er opties in het spel zijn.

De Monte Carlo simulatie heeft als grote voordeel dat de statistische verdeling van de mogelijke resultaten vrij gekozen kan worden. Door middel van trekkingen uit deze verdeling kunnen zowel rustige als onrustige perioden worden gesimuleerd. Nadelen van deze methode zijn dat de selectie van een verdeling en het schatten van de parameters een hoge moeilijkheidsgraad hebben. Verder is de berekening van de VaR met behulp van Monte Carlo simulatie voor grote portfolio's enorm tijdrovend.

De keuze voor één van deze methodes hangt af van de portefeuille waarvoor de VaR berekend moet worden. De historische simulatie en de Monte Carlo simulatie kunnen ook voor portefeuilles waarin opties voorkomen gebruikt worden, terwijl de variantie covariantie methode minder geschikt is wanneer er opties in het spel zijn. Bij een kleine hoeveelheid historische gegevens is het niet aan te raden om de historische simulatie te gebruiken. Tot slot is het bij historische simulatie niet mogelijk om de parameters aan te passen. Bij "stress testing", waarbij extreme marktomstandigheden worden onderzocht, zal de standaard deviatie en de correlaties worden aangepast en is het dus nodig om de variantie covariantie methode of Monte Carlo simulatie te gebruiken.

Om onderzoek te doen naar de Value-at-Risk en de gevolgen van het negeren van de parameteronzekerheid hebben wij de beschikking over enkele reeksen. Deze reeksen bestaan uit de dagelijkse slotkoersen van de indices van het CBS en de Standard & Poor 500 van 1 januari 1980 tot en met 3 september 1998.

De CBS-koersindex is de wetenschappelijke graadmeter van de Amsterdamse effectenbeurs. Deze index wordt tweemaal per dag door het Centraal Bureau voor de Statistiek berekend. Het is een gewogen index van alle in Amsterdam genoteerde aandelenkoersen met uitzondering van aandelen ten laste van vastgoedfondsen, beleggings- en houdster-maatschappijen (aandeelprijs maal het aantal uitstaande aandelen).

De S&P 500 Index is een gewogen index bestaande uit 500 aandelen geselecteerd op marktaandeel, liquiditeit en bedrijfstak. Het gewicht in de index is proportioneel met het marktaandeel.

Om statistische resultaten door de jaren heen te kunnen vergelijken worden de data eerst getransformeerd tot procentuele veranderingen van de indices. Deze transformatie wordt als volgt uit de oorspronkelijke data verkregen:

(1)

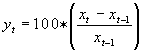
De term y_t geeft in deze formule de procentuele verandering weer en zal in het volgende hoofdstuk worden gebruikt om eigenschappen van de reeksen te bepalen en te analyseren. Verder is x_t de slotkoers van de betreffende index op tijdstip t.

In dit hoofdstuk bespreken wij de analyse van de reeksen CBS en S&P500 over de tijdsperiode van 1 januari 1980 tot en met 3 september 1998.

In de eerste paragraaf worden de gebruikte maatstaven besproken. Vervolgens passen wij deze maatstaven toe op de reeksen voor achtereenvolgens de gehele dataset, de dataset verdeeld in jaren en de dataset verdeeld in twee maandelijkse perioden.

Voor een goed inzicht in onze data hebben wij de volgende maatstaven geselecteerd: het minimum, het maximum, het gemiddelde, de standaard deviatie, de skewness en de kurtosis. Het minimum, het maximum, het gemiddelde en de standaard deviatie worden berekend met behulp van de bekend veronderstelde functies. De skewness(S) en de kurtosis(K) berekenen wij door gebruik te maken van de onderstaande functies.

(2)

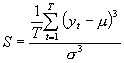
(3)

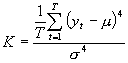
De skewness geeft aan in welke mate de verdeling scheef is ten opzichte van de normale verdeling. Als de skewness niet significant van nul verschilt, is de verdeling symmetrisch. Bij een negatieve skewness is de verdeling scheef naar links. Dit betekent dat de linker staart van de verdeling groter is dan de rechter. Indien de skewness positief is, dan is de verdeling scheef naar rechts.

De kurtosis geeft de steilheid ten opzichte van de normale verdeling weer. Indien de waarde niet significant van drie verschilt, is de steilheid van de verdeling gelijk aan die van de normale verdeling. Bij een grote kurtosis zijn er relatief veel waarden rond het gemiddelde ten opzichte van de normale verdeling. Een kurtosis kleiner dan drie geeft juist aan dat er relatief weinig waarnemingen rond het gemiddelde zijn.

Tot slot wordt met behulp van Eviews de kans berekend dat de reeks een normale verdeling heeft. Deze kans wordt weergegeven door de p-waarde van de Jarque-Bera toets op normaliteit. Bij een p-waarde kleiner dan 5% wordt de veronderstelling van een normale verdeling verworpen .

Als eerste bespreken wij de resultaten verkregen uit onderzoek van de totale dataset. Deze staan vermeld in tabel 1.

Het minimum en maximum worden weergegeven in procenten per dag, terwijl het gemiddelde en de standaard deviatie worden uitgedrukt in procenten per jaar.

Uit deze tabel kunnen wij het volgende concluderen. Allereerst zien we dat het gemiddelde rendement van de CBS-index groter is dan het gemiddelde van de S&P500-index. Tegenover dit grotere rendement van de CBS staat ook een groter risico. Dat dit risico zwaar meeweegt, is te zien aan het 95%-betrouwbaarheidsinterval voor de CBS-index (-1.82, 1.97) en (-1.79, 1.92) voor de S&P500-index.

Verder valt op dat vooral voor de S&P500 het minimum in absolute waarde groter is dan het maximum. Dit in combinatie met het positieve gemiddelde duidt erop dat er meer stijgingen dan dalingen voorkomen. Tevens valt te concluderen dat de dalingen tijdens een crash groter zijn dan de stijgingen tijdens een "recovery period". Echter zal een "recovery period" over het algemeen langer aanhouden, hetgeen verklaart dat er meer stijgingen dan dalingen in de reeks zullen zijn.

De negatieve waarde van de skewness duidt op een verdeling met zwaardere staarten aan de linkerzijde, voor beide reeksen. Tot slot geeft de grote positieve waarde van de kurtosis aan dat de kromming van de verdelingen erg steil is. De p-waarde van de Jarque-Bera toets op normaliteit is 0.00 voor beide reeksen, waardoor de hypothese dat de reeks normaal verdeeld is voor beide indices verworpen wordt.

Om te onderzoeken of er perioden van verschillende volatiliteit zijn geweest, of dat de volatiliteit misschien redelijk constant over de tijd verloopt, verdelen wij nu de gehele dataset in jaarlijkse perioden. Deze resultaten zijn te zien in bijlage I.

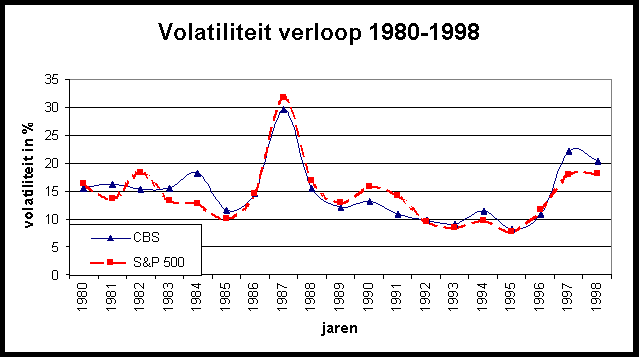
Het eerste punt dat opvalt is dat de volatiliteit in 1987 opvallend groot is voor beide reeksen als gevolg van de grote onrust rond de beurscrash op 19 oktober van dat jaar. Verder is er een periode van betrekkelijke rust waar te nemen tussen 1992 en 1996. Dit gevolgd door een plotselinge grote toename in 1997 en 1998. Dit is geïllustreerd in figuur 1. Uit de tabel en de grafiek valt te concluderen dat het verloop van de volatiliteit over de jaren heen niet constant is.

Het verloop van de indices volgt een Brownse beweging, waardoor geen voorspellingen voor gemiddelden kunnen worden gedaan. Dit verklaart de uiteen-lopende gemiddelde rendementen in de tabel. Er is wel iets af te lezen over de economische situaties in de betreffende jaren, zoals grote groei in 1983, 1988, 1993, 1996 en 1997 voor de CBS-index. Voor de S&P500 zien wij opvallende groei in de jaren '80, '85, '89, '91, '95 en '97. Dalingen zijn te vinden in 1987 en 1990 voor de CBS-index en in '81 en '90 voor de S&P500.

Om te onderzoeken of de volatiliteit binnen een jaar ook een ongelijkmatig verloop vertoont, hebben wij de datareeksen in 2-maandelijkse perioden verdeeld. We doen dit van januari 1980 tot en met augustus 1998 en bepalen voor elke periode van 2 maanden het gemiddelde van deze maatstaven. Voor de gemiddelde volatiliteit bepalen we tevens de spreiding, welke wordt weergegeven door de standaard deviatie. Het minimum en maximum worden uitgedrukt in dagpercentages, terwijl het gemiddeld rendement en de gemiddelde volatiliteit worden uitgedrukt in procenten per jaar. De standaard deviatie van de gemiddelde volatiliteit wordt ook in procenten per jaar uitgedrukt. De resultaten staan vermeld in onderstaande tabellen.

We zien dat voor beide indices de gemiddelde volatiliteit en de bijbehorende standaard deviatie in de maanden september en oktober aanmerkelijk groter is dan in de overige perioden. Verder is het gemiddeld rendement in deze periode aanzienlijk kleiner. Dit betekent dat deze periode als erg onrustig kan worden gekenmerkt. De maanden mei en juni daarentegen kunnen als betrekkelijk rustig worden gekenmerkt, vanwege het behoorlijk hoge gemiddelde rendement en de relatief lage volatiliteit. Bovendien is de standaard deviatie van de gemiddelde volatiliteit erg klein, waardoor deze met redelijke zekerheid kan worden voorspeld.

In dit hoofdstuk zullen we op basis van de bovenstaande methoden en resultaten de waarde van de Value-at-Risk bepalen. Voor de gehele dataset doen we dit voor alledrie de besproken methoden, terwijl voor de jaarlijkse en 2-maandelijkse perioden alleen de variantie covariantie methode en de Monte Carlo Simulatie worden toegepast. De historische simulatie wordt niet meer gebruikt, omdat de hoeveelheid gegevens te klein wordt. Monte Carlo Simulatie wordt uitgevoerd op grond van de normale verdeling, ondanks dat deze in het voorgaande hoofdstuk is verworpen. In het eindverslag wordt nader onderzoek gedaan naar de juiste verdeling van de twee indices.

Voor de gehele dataset bepalen we de Value-at-Risk op basis van historische simulatie, de variantie-covariantie methode en Monte Carlo simulatie, welke beschreven staan in het eerste hoofdstuk. De verkregen resultaten worden voor zowel de CBS als de S&P500 vermeld in tabel 2 tot en met 4:

De Monte Carlo simulatie methode en de Variantie-covariantie methode geven niet significant verschillende waarden, terwijl de historisch simulatie methode verschilt ten opzichte van de andere twee methoden. De werkelijke verdeling is meer gecentreerd rond zijn gemiddelde en heeft enkele grote uitschieters t.o.v. de normale verdeling, welke wordt verondersteld door de VC Methode en de MC Simulatie. Dit heeft als gevolg dat bij de historische simulatie de 1% VaR aanmerkelijk kleiner is en de 5% VaR groter is, dan de betreffende waarden van de andere methoden.

In eerste instantie zullen we de waarde van de verschillende VaR-percentages bepalen voor jaarlijkse perioden. De in paragraaf 3.2 verkregen volatiliteiten worden gebruikt om met behulp van de VC Methode en MC Simulatie de waarde van de VaR te bepalen. Deze resultaten worden weergegeven in de tabellen in bijlage II.

Opvallend is het verschil in VaR in het jaar 1987 voor de CBS-index. In dit jaar was er een grote volatiliteit en de beroemde beurscrash. De mogelijkheid tot dergelijke grote dalingen komen in de VaR-waarde van de VC Methode aanmerkelijk beter tot uitdrukking dan bij MC Simulatie. Voor de S&P500 geeft Monte Carlo Simulatie een beter inzicht in de grote spreiding van dat jaar. De 1% VaR is in dit geval ongeveer gelijk aan de 1% VaR berekend met behulp van de VC Methode.

Verder kan de periode van 1992 tot en met 1996 worden gekenmerkt als een periode van relatief laag risico. Gedurende de laatste 2 jaar echter is dit risico weer aanzienlijk toegenomen.

In tweede instantie wordt de verhouding van de risico's binnen een jaar bekeken door gebruik te maken van 2-maandelijkse perioden. De Value-at-Risk wordt bepaald o.b.v. het gemiddelde van de volatiliteiten van de betreffende periode over de jaren 1980 tot en met 1998. Verder kan met behulp van de spreiding van de gemiddelde volatiliteit de nauwkeurigheid van de Value-at-Risk worden weergeven. De verkregen resultaten staan vermeld in de tabellen 7 en 8.

Net als in hoofdstuk 3 kunnen we hier concluderen dat de maanden september en oktober relatief grote risico's bevatten ten op zichte van de andere perioden. De maanden mei en juni daarentegen kunnen als redelijk risicoloos worden beoordeeld.

In paragraaf 3.2.3 hebben we gezien dat de volatiliteit in 2-maandelijkse perioden sterk kan variëren. Nu zullen we onderzoeken welke gevolgen deze onzekerheid in de volatiliteit heeft voor de waarde van de Value-at-Risk. Met behulp van de centrale limietstelling construeren we voor iedere 2-maandelijkse periode een 95% betrouwbaarheidsinterval voor de volatiliteit. Met behulp van de onder- en bovengrens van de volatiliteit, berekenen we de onder- en bovengrens van de VaR voor zowel de variantie covariantie methode als Monte Carlo simulatie. De resultaten staan in onderstaande tabellen.

In voorgaande paragraaf is de 2-maandelijkse VaR gebaseerd op de gemiddelde volatiliteit voor de betreffende periode van 1980 t/m 1998. De gevolgen van het negeren van de onzekerheid in deze volatiliteit voor de VaR komen in bovenstaande tabellen nadrukkelijk naar voren. Het is duidelijk dat de keuze van de methode invloed heeft op de grootte van het interval. De variantie covariantie methode geeft in alle gevallen een groter interval dan de Monte Carlo simulatie.

De onzekerheid in de volatiliteit leidt tot onzekerheid in de Value-at-Risk. Bij het gebruik van het gemiddelde is het mogelijk dat het risico onderschat wordt. Door de ondergrens van het betrouwbaarheidsinterval te nemen, wordt een groot deel van dit risico weggenomen. De waarden in tabellen 7 en 8 worden dan vervangen door de waarden in de kolommen ondergrens in tabellen 9 tot en met 12.

In voorgaande hoofdstukken hebben we kunnen zien dat de volatiliteit per periode verschilt. Dit zou een indicatie kunnen zijn voor conditionele heteroskedasticiteit in de data. Dit houdt in dat de volatiliteit niet constant over de tijd is en afhangt van de historische volatiliteit. De gedachte hierachter is, dat in erg volatiele perioden er een grotere onzekerheid is over de volgende observatie dan in perioden met een kleinere volatiliteit.

De bedoeling is om met behulp van de te bespreken modellen in paragraaf 5.2 een betere schatting van de volatiliteit te geven. Met deze nieuwe volatiliteiten kunnen we nauwkeuriger Value-at-Risk berekenen. Dit zal pas in het eindverslag gepresenteerd worden.

In paragraaf 1 testen we beide reeksen op de aanwezigheid van conditionele heteroskedasticiteit. In paragraaf twee bespreken we de theorie achter de ARCH en GARCH modellen.

De aanwezigheid van conditionele heteroskedasticiteit zullen we toetsen met behulp van een eenvoudige LM-toets. De nulhypothese veronderstelt dat er geen conditionele heteroskedasticiteit in het model aanwezig is, terwijl de alternatieve hypothese dit juist wel aanneemt.

De waarde van deze LM-test is gegeven door het aantal waarnemingen te vermenigvuldigen met de R² van de hulpregressie

waarbij û_t² de gekwadrateerde residuen zijn van de ARMA tijdreeks. Deze test heeft een Chi-kwadraat verdeling met q vrijheidsgraden. De nulhypothese wordt met 95% zekerheid verworpen als de p-waarde van deze test 0.05 is.

Wij gebruiken de LM-test om te onderzoeken of de reeksen conditionele heteroskedasticiteit bevatten door q gelijk te stellen aan 1. De gekwadrateerde residuen worden verkregen uit de tijdreeks y_t = a + b y_t-1 + e _t. Deze test is uitgevoerd met behulp van het statistische programma Econometric Views 2.0.

Voor zowel de CBS index als de Standard & Poor 500 index is de p-waarde gelijk aan 0. De nulhypothese: "geen conditionele heteroskedasticiteit" wordt dus voor beide reeksen met meer dan 95% zekerheid verworpen. Om later tot het voorspellen van de volatiliteit over te gaan, zal gebruik gemaakt moeten worden van ARCH of GARCH modellen.

Om accurate voorspellingen te maken, zullen we gebruik maken van een model met conditionele heteroskedasticiteit. Daarbij bestaat de keuze tussen een Autoregressive Conditional Heteroscedasticity model(ARCH) en een Generalized Autoregressive Conditional Heteroscedasticity model(GARCH). Het ARCH(q) model wordt beschreven door formules 5, 6 en 7.

(5)

(6)

(7)

 

Het GARCH(p, q) model wordt gegeven door de volgende drie vergelijkingen:

 

(8)

 

(9)

(10)

Voor financiële tijdreeksen blijkt, dat de waarde van q in vergelijking (10) veel kleiner is dan de waarde in vergelijking (7), zodat er minder parameters geschat hoeven te worden. Vaak geeft het GARCH(1,1) model een adequate beschrijving voor veel financiële tijdreeksen.

In dit rapport hebben we Value-at-Risk uitgelegd en bespraken we drie verschillende methoden om Value-at-Risk te berekenen. Deze methoden hebben we losgelaten op twee reeksen te weten de CBS-koersindex en de S&P500 index. Aan de hand van dat onderzoek kunnen we de volgende conclusies trekken.

Value-at-Risk wordt gebaseerd op gegevens uit het verleden. Onzekerheden moeten zoveel mogelijk worden meegenomen in de bepaling van de VaR. De belangrijkste variabele in de berekening van de Value-at-Risk is de volatiliteit. Indien een goede schatting van de volatiliteit gegenereerd kan worden, is een goede schatting van de VaR mogelijk. De onderliggende waarde waarvoor de VaR berekend wordt, moet dus allereerst aan een degelijk onderzoek naar de juiste verdeling en zijn volatiliteit worden onderworpen. Het risico van onderschatting kan grotendeels worden weggenomen door gebruik te maken van de ondergrens van het betrouwbaarheidsinterval van de Value-at-Risk.

In het vervolg zullen we dieper ingaan op de parameteronzekerheid in Value-at-Risk. Voor een goede schatting van de volatiliteit onderzoeken wij de resultaten van de ARCH of GARCH modellen. Indien deze modellen geen bevredigende resulaten leveren, wordt gezocht naar meer geschikte modellen. Uiteindelijk wordt de voorspelling van de Value-at-Risk getoetst aan de hand van de gegevens van na 3 september 1998.

Greene, W.H. (1997), Econometric Analysis, Prentice Hall International

	Min	Max	Gemiddelde		Volatiliteit
Periode	(%)	(%)	Dag (%)	Jaar (%)	Dag (%)	Jaar (%)
1980	-2.80	3.12	0.08	19.29	0.97	15.45
1981	-3.06	3.35	0.00	0.75	1.03	16.31
1982	-2.54	4.11	0.09	22.04	0.97	15.42
1983	-3.21	3.38	0.19	47.10	0.98	15.50
1984	-4.28	3.80	0.09	23.48	1.15	18.30
1985	-2.13	2.73	0.11	28.29	0.73	11.64
1986	-3.01	5.27	0.04	9.82	0.92	14.59
1987	-11.18	10.50	-0.06	-14.59	1.87	29.70
1988	-4.07	5.44	0.12	30.35	0.98	15.54
1989	-5.71	1.72	0.10	24.30	0.76	12.13
1990	-2.81	2.93	-0.05	-12.70	0.84	13.30
1991	-3.64	2.62	0.07	17.17	0.69	10.89
1992	-2.96	2.92	0.03	7.81	0.62	9.77
1993	-1.72	1.36	0.15	37.79	0.57	9.02
1994	-2.56	1.96	0.01	2.85	0.73	11.51
1995	-1.46	1.65	0.07	17.86	0.51	8.13
1996	-2.35	1.62	0.13	33.21	0.69	10.97
1997	-4.08	5.25	0.15	38.29	1.40	22.18
1998	-4.54	4.78	0.08	20.32	1.29	20.40

	Min	Max	Gemiddelde		Volatiliteit
Periode	(%)	(%)	Dag (%)	Jaar (%)	Dag (%)	Jaar (%)
1980	-2.99	3.66	0.11	28.59	1.03	16.33
1981	-2.87	2.67	-0.02	-4.00	0.85	13.56
1982	-3.95	4.78	0.08	20.52	1.15	18.25
1983	-2.68	2.72	0.08	20.58	0.83	13.21
1984	-1.80	2.79	0.03	6.64	0.80	12.63
1985	-1.44	2.30	0.11	27.19	0.63	9.99
1986	-4.80	2.27	0.07	17.60	0.91	14.48
1987	-20.40	9.11	0.04	10.21	1.99	31.60
1988	-6.76	3.60	0.06	16.23	1.06	16.80
1989	-6.11	2.78	0.11	27.54	0.81	12.86
1990	-3.01	3.20	-0.01	-1.83	0.99	15.71
1991	-3.65	3.75	0.11	26.70	0.89	14.09
1992	-1.85	1.57	0.03	7.54	0.60	9.53
1993	-2.39	1.94	0.04	9.63	0.53	8.47
1994	-2.26	2.15	0.01	1.69	0.61	9.69
1995	-1.54	1.89	0.12	31.24	0.48	7.69
1996	-3.07	1.95	0.08	20.55	0.73	11.60
1997	-6.86	5.12	0.12	29.40	1.12	17.85
1998	-6.80	3.87	0.02	4.80	1.13	18.01